Mencari Dimensi
- Category: Fisika X SMA
- Written by fisikastudycenter
Mencari dimensi suatu besaran?
Dimensi dari gaya?
Dimensi dari daya?
Dimensi dari energi?
Dimensi dari impuls?
Dimensi dari momentum?

Dengan asumsi bahwa beberapa rumus belum diketahui pelajar X SMA, kecuali panjang (m), massa (kg), waktu (s), kecepatan (m/s), percepatan (m/s2), luas (m2) dan volume (m3) yang diasumsikan sudah diketahui, berikut penurunan beberapa dimensi besaran Fisika sederhana.
Format disini adalah :
Rumus ---> Satuan --> Dimensi
dan ingat :
massa --> kg --> M ( dari Mass kali..!?! & jangan kliru Meter..!!!)
panjang --> m --> L ( dari Length kali...!?! )
waktu --> s --> T ( dari Time kali...!!! )
Gaya
massa x percepatan--> (kg) (m/s2) --> M L T − 2
Massa Jenis
massa / volume --> (kg)/(m3) --> M L−3
Energi
massa x percepatan gravitasi x tinggi --> (kg)(m/s2)(m) --> M L2 T − 2
Tekanan
gaya/luas ---> (kg)(m/s2)/m2 --> M L −1 T −2
Usaha
gaya x perpindahan--> (kg)(m/s2)(m)--> M L2 T −2
Momentum
massa x kecepatan --> (kg)(m/s) --> M L T −1
Impuls
gaya x selang waktu --> (kg)(m/s2)(s) --> M L T −1
Daya
Usaha/waktu --> (kg)(m/s2)(m)/(s) - -> M L 2 T −3
Berat
massa x percepatan gravitasi --> (kg)(m/s2) --> M L T −2
Berat Jenis
berat/volume --> (kg)(m/s2)/(m3) --> M L −2 T −2
Beberapa besaran memiliki kesamaan dimensi, seperti Usaha dan Energi, Gaya dan Berat, Impuls dan momentum.
Untuk soal yang sedikit lebih rumit biasanya ditampilkan rumusnya, tinggal otak-atik, pindah kanan kiri, atas bawah, masukkan satuannya baru dikonvert ke dimensi.
Sekedar Contoh:
Diberikan formula gaya gravitasi antara dua benda sebagai berikut

dengan F adalah gaya (Newton) m1 dan m2 adalah massa kedua buah benda (kg), r adalah jarak kedua benda (m) dan G adalah suatu konstanta yang akan dicari dimensinya.
Dari rumus diatas setelah dibolak-balik didapatkan bahwa
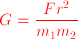
masukkan satuannya bawa ke kg, m dan s. Untuk satuan gaya lihat daftar diatas, didapat
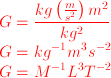
Contoh berikutnya:
Diberikan persamaan gaya pegas
F = k Δ X
Dimana F adalah gaya pegas (Newton), Δ X adalah pertambahan panjang pegas (meter) dan k adalah konstanta pegas. Dimensi konstanta pegas?

Lanjut,.. berikutnya bagaimana memeriksa benar tidaknya suatu persamaan yang menghubungkan besaran-besaran tertentu (memeriksa rumus) dengan analisis dimensi atau rumus seperti dua contoh berikut ini:
1) Persamaan berikut menghubungkan besaran-besaran pada gerak suatu benda.
vt = vo + at
dimana vt adalah kecepatan saat t, vo adalah kecepatan awal, a adalah percepatan dan t adalah waktu.
Periksa dengan analisis dimensi benar tidaknya persamaan diatas!
2) Kedudukan suatu benda dinyatakan dalam suatu persamaan
y = At2 + Bt + C
dengan satuan y dalam meter, dan t dalam sekon. A, B dan C adalah konstanta-konstanta. tentukan satuan dan dimensi dari A, B dan C! (Soal Fisikastudycenter)
Pembahasan
1) Dimensi pada ruas kiri:
vt adalah kecepatan → m/s → L/T → LT−1
Dimensi pada ruas kanan:
vo adalah kecepatan → m/s → L/T → LT−1
at adalah percepatan x waktu → m/s2 x s → m/s → L/T → LT−1
Terlihat dimensi ruas kiri sama dengan dimensi pada ruas kanan, sehingga persamaan di atas adalah tepat.
2) Asumsinya adalah besaran-besaran yang dijumlahkan atau dikurangkan memiliki satuan atau dimensi yang sama dengan hasilnya. Dari persamaan
y = At2 + Bt + C
...meter = ...meter + ...meter + ...meter
Menentukan satuan konstanta A
Hasil kombinasi satuan-satuan pada At2 haruslah meter, masukkan satuan-satuan lain yang telah diketahui dalam hal ini t (waktu) satuannya adalah s (sekon) sehingga
At2 = m
As2 = m
A = m/s2
Dimensi A adalah LT−2
Menentukan satuan konstanta B
Bt juga menghasilkan meter, masukkan satuan lain yang telah diketahui sehingga
Bt = m
Bs = m
B = m/s
Dimensi dari B adalah LT−1
Menentukan satuan konstanta C
C = m
Dimensi C adalah L
Dimensi dari gaya?
Dimensi dari daya?
Dimensi dari energi?
Dimensi dari impuls?
Dimensi dari momentum?

Dengan asumsi bahwa beberapa rumus belum diketahui pelajar X SMA, kecuali panjang (m), massa (kg), waktu (s), kecepatan (m/s), percepatan (m/s2), luas (m2) dan volume (m3) yang diasumsikan sudah diketahui, berikut penurunan beberapa dimensi besaran Fisika sederhana.
Format disini adalah :
Rumus ---> Satuan --> Dimensi
dan ingat :
massa --> kg --> M ( dari Mass kali..!?! & jangan kliru Meter..!!!)
panjang --> m --> L ( dari Length kali...!?! )
waktu --> s --> T ( dari Time kali...!!! )
Gaya
massa x percepatan--> (kg) (m/s2) --> M L T − 2
Massa Jenis
massa / volume --> (kg)/(m3) --> M L−3
Energi
massa x percepatan gravitasi x tinggi --> (kg)(m/s2)(m) --> M L2 T − 2
Tekanan
gaya/luas ---> (kg)(m/s2)/m2 --> M L −1 T −2
Usaha
gaya x perpindahan--> (kg)(m/s2)(m)--> M L2 T −2
Momentum
massa x kecepatan --> (kg)(m/s) --> M L T −1
Impuls
gaya x selang waktu --> (kg)(m/s2)(s) --> M L T −1
Daya
Usaha/waktu --> (kg)(m/s2)(m)/(s) - -> M L 2 T −3
Berat
massa x percepatan gravitasi --> (kg)(m/s2) --> M L T −2
Berat Jenis
berat/volume --> (kg)(m/s2)/(m3) --> M L −2 T −2
Beberapa besaran memiliki kesamaan dimensi, seperti Usaha dan Energi, Gaya dan Berat, Impuls dan momentum.
Untuk soal yang sedikit lebih rumit biasanya ditampilkan rumusnya, tinggal otak-atik, pindah kanan kiri, atas bawah, masukkan satuannya baru dikonvert ke dimensi.
Sekedar Contoh:
Diberikan formula gaya gravitasi antara dua benda sebagai berikut

dengan F adalah gaya (Newton) m1 dan m2 adalah massa kedua buah benda (kg), r adalah jarak kedua benda (m) dan G adalah suatu konstanta yang akan dicari dimensinya.
Dari rumus diatas setelah dibolak-balik didapatkan bahwa
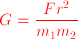
masukkan satuannya bawa ke kg, m dan s. Untuk satuan gaya lihat daftar diatas, didapat
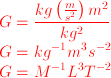
Contoh berikutnya:
Diberikan persamaan gaya pegas
F = k Δ X
Dimana F adalah gaya pegas (Newton), Δ X adalah pertambahan panjang pegas (meter) dan k adalah konstanta pegas. Dimensi konstanta pegas?

Lanjut,.. berikutnya bagaimana memeriksa benar tidaknya suatu persamaan yang menghubungkan besaran-besaran tertentu (memeriksa rumus) dengan analisis dimensi atau rumus seperti dua contoh berikut ini:
1) Persamaan berikut menghubungkan besaran-besaran pada gerak suatu benda.
vt = vo + at
dimana vt adalah kecepatan saat t, vo adalah kecepatan awal, a adalah percepatan dan t adalah waktu.
Periksa dengan analisis dimensi benar tidaknya persamaan diatas!
2) Kedudukan suatu benda dinyatakan dalam suatu persamaan
y = At2 + Bt + C
dengan satuan y dalam meter, dan t dalam sekon. A, B dan C adalah konstanta-konstanta. tentukan satuan dan dimensi dari A, B dan C! (Soal Fisikastudycenter)
Pembahasan
1) Dimensi pada ruas kiri:
vt adalah kecepatan → m/s → L/T → LT−1
Dimensi pada ruas kanan:
vo adalah kecepatan → m/s → L/T → LT−1
at adalah percepatan x waktu → m/s2 x s → m/s → L/T → LT−1
Terlihat dimensi ruas kiri sama dengan dimensi pada ruas kanan, sehingga persamaan di atas adalah tepat.
2) Asumsinya adalah besaran-besaran yang dijumlahkan atau dikurangkan memiliki satuan atau dimensi yang sama dengan hasilnya. Dari persamaan
y = At2 + Bt + C
...meter = ...meter + ...meter + ...meter
Menentukan satuan konstanta A
Hasil kombinasi satuan-satuan pada At2 haruslah meter, masukkan satuan-satuan lain yang telah diketahui dalam hal ini t (waktu) satuannya adalah s (sekon) sehingga
At2 = m
As2 = m
A = m/s2
Dimensi A adalah LT−2
Menentukan satuan konstanta B
Bt juga menghasilkan meter, masukkan satuan lain yang telah diketahui sehingga
Bt = m
Bs = m
B = m/s
Dimensi dari B adalah LT−1
Menentukan satuan konstanta C
C = m
Dimensi C adalah L
Read more: http://fisikastudycenter.com/fisika-x-sma/1-mencari-dimensi#ixzz268gPyla8
mana lagi mas
BalasHapus